Chapter 5 Basic Nonlinear Time Series Analysis
Many nonlinear analyses can be considered “descriptive” techniques, that is, the aim is not to fit the parameters of a model, but to describe, quantitatively, some aspects of how one value changes into another value over time.
5.0.1 Intuitive notion of Fractal Dimension
You are probably familiar with the notion of dimension, that is, the notion displayed in Figure 5.1 a point has dimension 0, a line dimension 1, a plane dimension 2 and a cube dimension 3.
Figure 5.1: “By NerdBoy1392 - Own work, CC BY-SA 3.0, Link”
The fractal dimension of an object indicates how much it ‘spills over’ into the next integer dimension. Mathematician Benoît B. Mandelbrot used it to (formally) study the roughness of the world, which was quite revolutionary in mathematics where everything is neat and smooth.
A qualitative description of the fractal dimension of a time series (or 1D curve) can be given by deciding whether the curve looks/behaves like a line, or, like a plane.
As can be seen in the Figure 5.2, if slow processes (low frequencies) dominate the signal, they are more line-like (bottom of the figure) and will have a fractal dimension closer to 1. If fast processes (high frequencies) dominate the signal, they are more plane-like and will have a fractal dimension closer to 2.
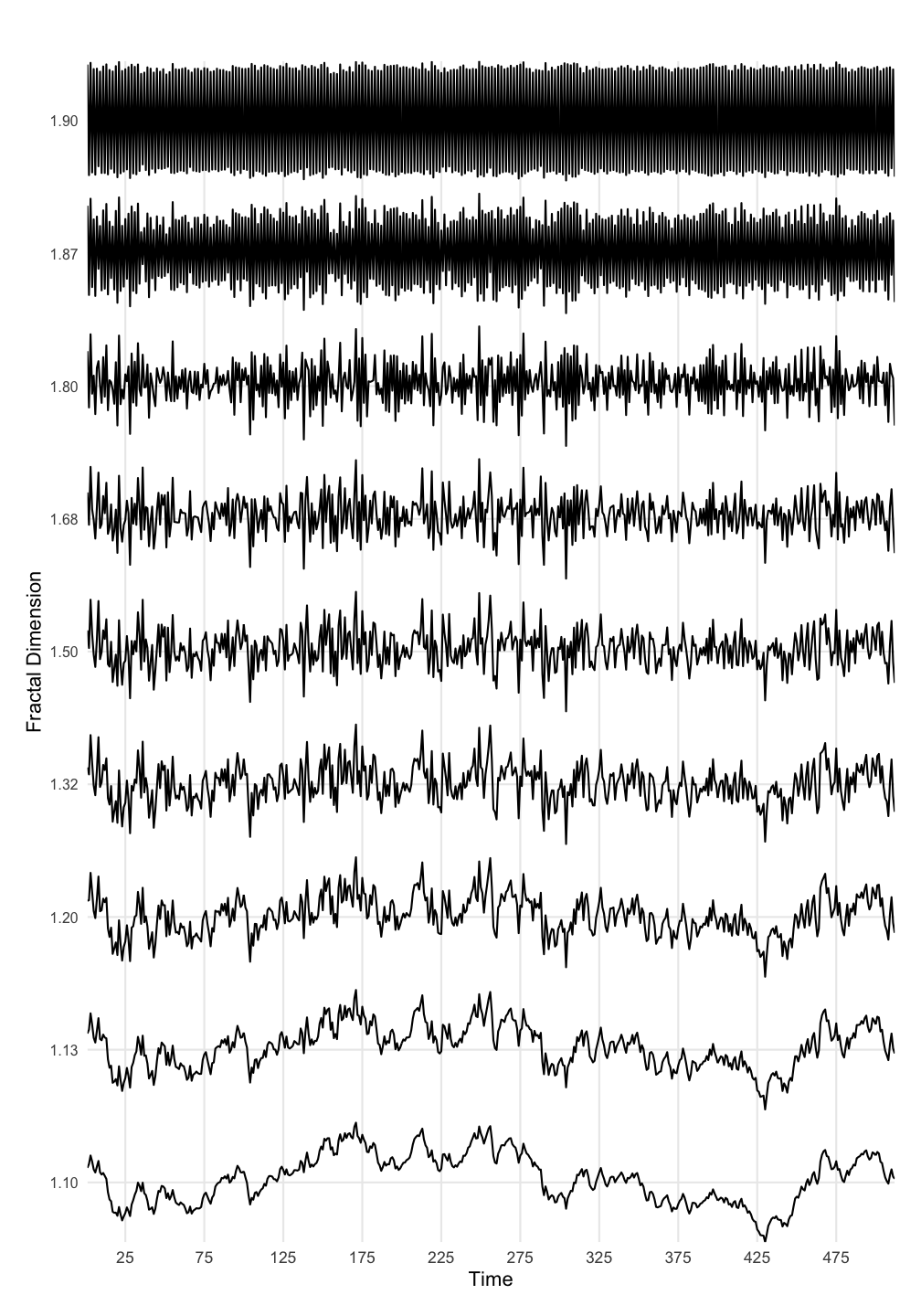
Figure 5.2: The fractal dimension of different types of change processes
5.0.2 Coloured noise
You can also think of these different types of time-series as being generated by different kinds of processes, they have a different type of correlational structure, what varies is at which time scales the largest correlations can be found. So let’s study the correlation functions of these noises, which are often denoted by a colour based on the [colours of the visible light spectrum](https://en.wikipedia.org/wiki/Colors_of_noise.
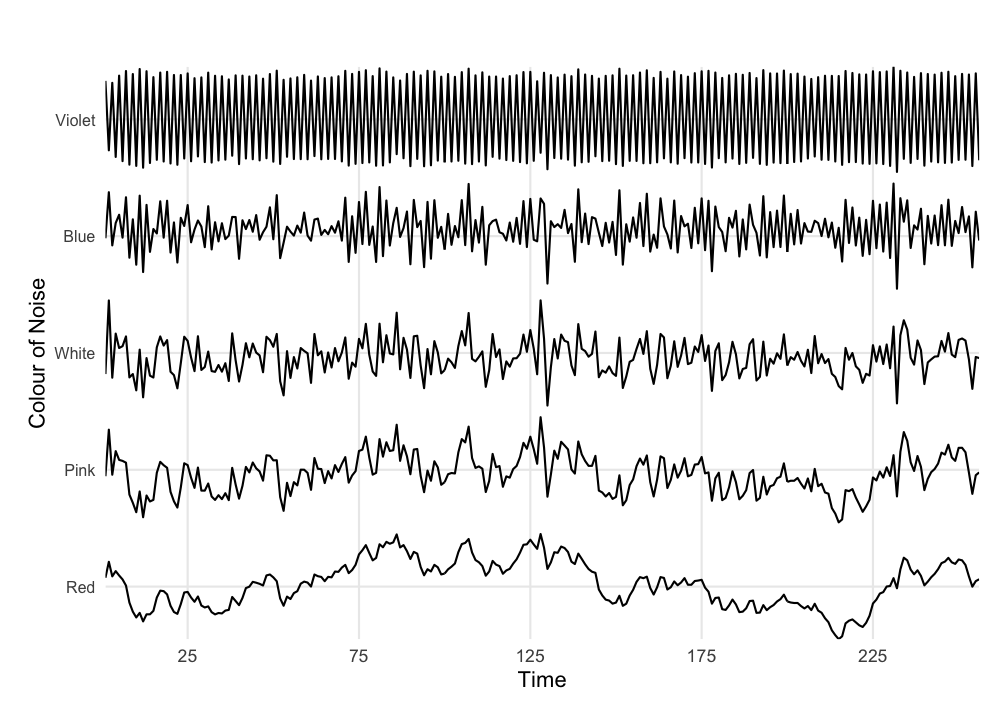
5.0.2.1 Brownian (red) noise
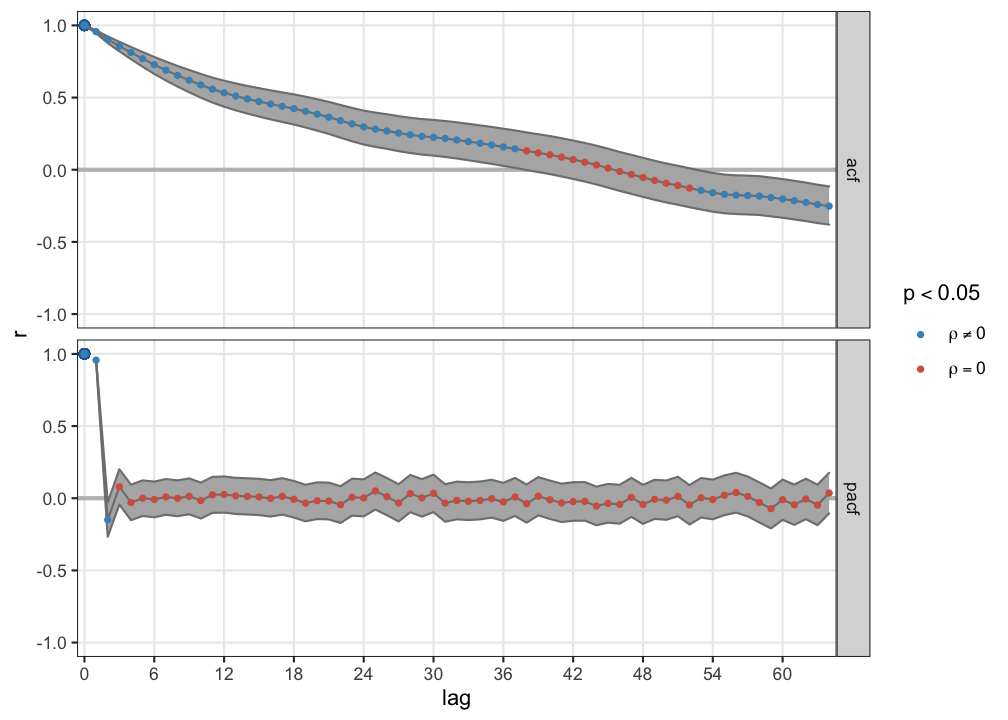
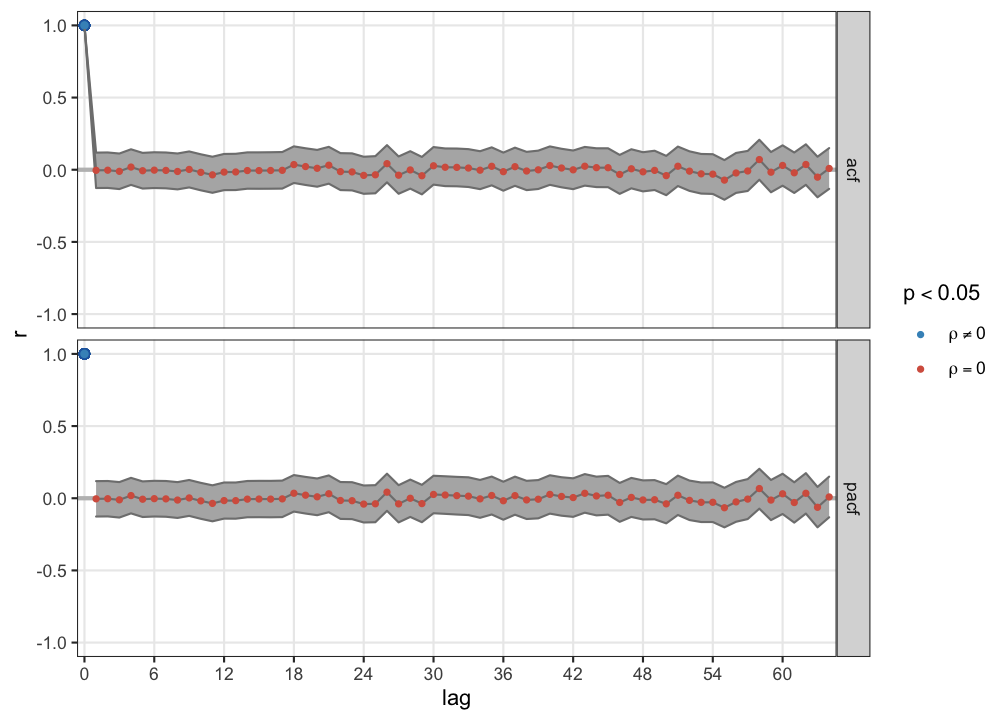
Persistent pattern, correlations exist at all lags, but in the partial acf at lag 1 \(r \approx 1\). Brownian noise is the cumulative sum of white noise, a random walk.
Violet noise
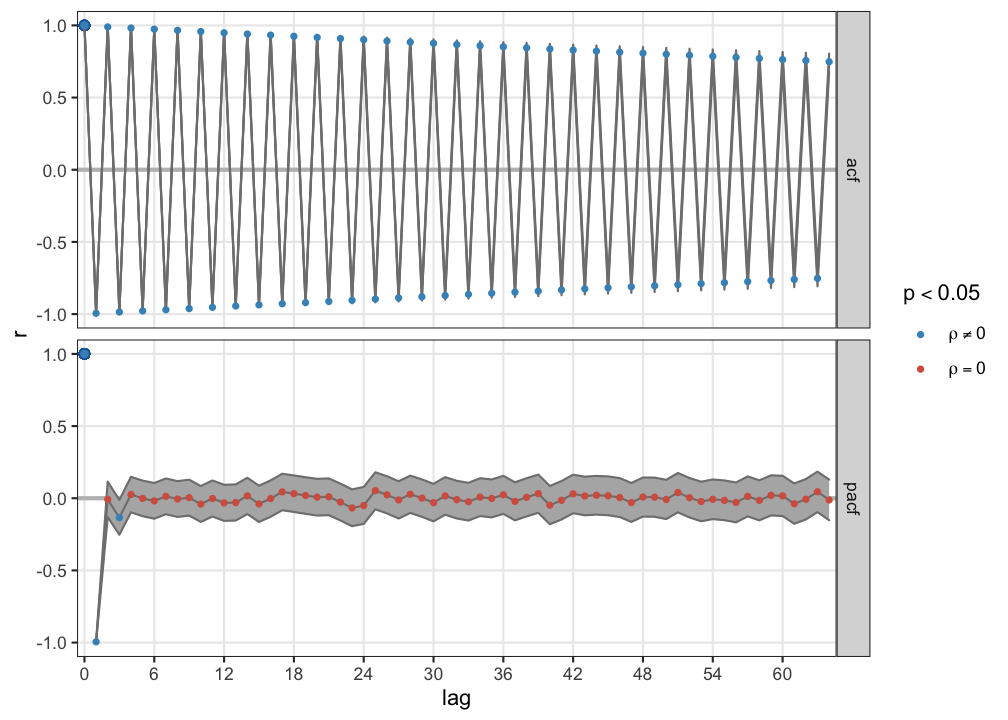
Anti-persistent pattern, correlations exist at all lags, but they change sign. In the partial acf at lag 1 \(r \approx -1\).
Fractals
You have probably heard about fractals as being objects that are made out of little copies of the whole, self-similar objects. The video below provides a good introduction to what fractals are and what they are not, what the fractal dimension actually means and it introduces the concept of **roughness, scaling* and box-counting dimension. We will eventually discuss all these topics, for now it is ok to stop after about 10 minutes.