Chapter 9 Unordered Categorical Data

The basic principles behind all varieties of Recurrence Quantification Analysis can be explained by looking at simple examples based on unordered categorical data (nominal time series).

Let’s consider this poem and regard interpret it as a time series (or perhaps better, an event series):

One little bear
Wondering what to do
Along came another
Then there were two!

Two little bears
Climbing up a tree
Along came another
Then there were three!

Three little bears
Ate an apple core
Along came another
Then there were four!

Four little bears
Found honey in a hive
Along came another
Then there were five!

We can assign a number to each unique word in the poem. The absolute value of the numbers in the series have no meaning, but what we can say is that whenever a number is repeated, this means a word was repeated. If a specific sequence of numbers is repeated, a larger pattern of words was repeated.

To change the poem into a time series we can use the function casnet::as.numeric_discrete() on a vector that contains the individual words, in lower case, without any punctuation symbols. It returns a named numeric vector, the names will be the words of the poem.

library(casnet)
bear1 <- c("one little bear wondering what to do along came another then there were two two little bears climbing up a tree along came another then there were three three little bears ate an apple core along came another then there were four four little bears found honey in a hive along came another then there were five")

bear_up <- as.numeric_discrete(unlist(strsplit(bear1," ")))

plot(bear_up, type = "b", xlab = "Time", ylab = "Unique Word", pch = 16)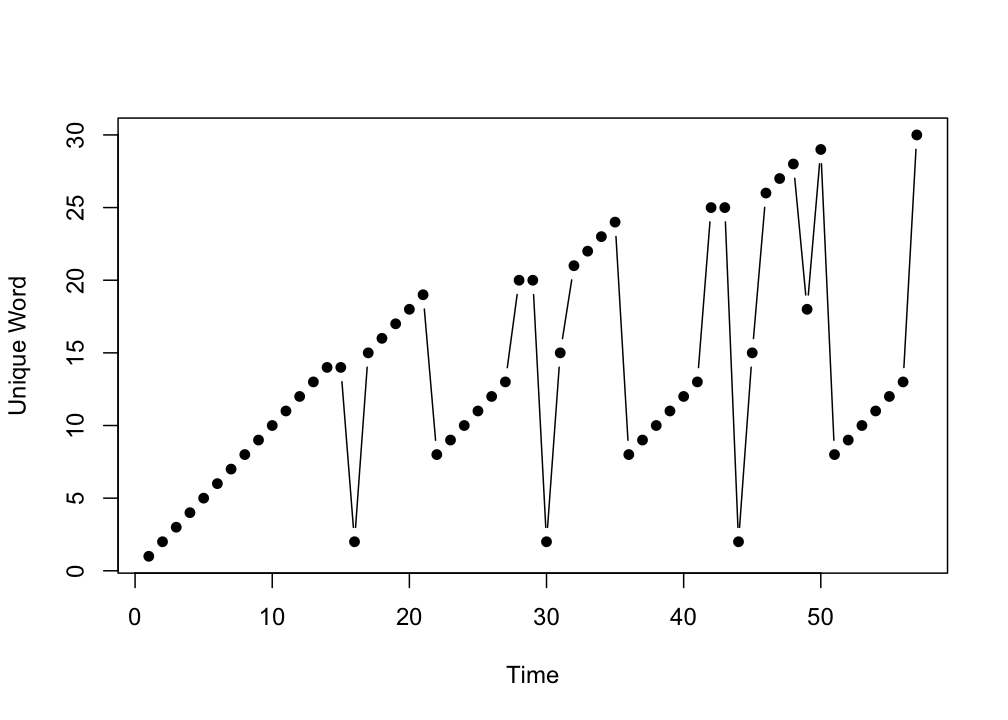

Several things can be inferred from the plot of the time series :

• At Time = 15 the same word is repeated (horizontal line). This is actually due to the omission of the punctuation symbols, it is the repetition of the word "two" which was at the end of one sentence and at the beginning of the next sentence.
  
• At Time = 16 for the first time a non-identical unique word is repeated ("little").
  
• At several points there are larger patterns that are repeated ("along came another then there were").
  
• The last word of the poem is in fact a unique word ("five")

How can we quantify these features of the poem? How can we quantify these dynamic patterns?