5.1 Relative Roughness

Relative Roughness evaluates the local variability relative to the global variability in a time series. It is calculated using the following formula:

\[\begin{equation} RR = 2*\left[1 - \frac{\gamma_1(x_i)}{Var(x_i)}\right] \tag{5.1} \end{equation}\]

The numerator in the formula stands for the lag 1 auto-covariance of the time series \(x_i\), this is the unstandardised lag1 autocorrelation (auto-covariance). The denominator stands for the (global) variance of \(x_i\) which all statistics packages can calculate. Another way to describe the global variance is: lag 0 auto-covariance.

You can use Figure 5.3 to lookup which value of \(RR\) corresponds to which fractal dimension. The line-like time series will have low local variance and high global variance and therefore the Relative roughness will be small. The plane-like time series will have high local variance and low global variance, resulting in a high value for Relative Roughness.

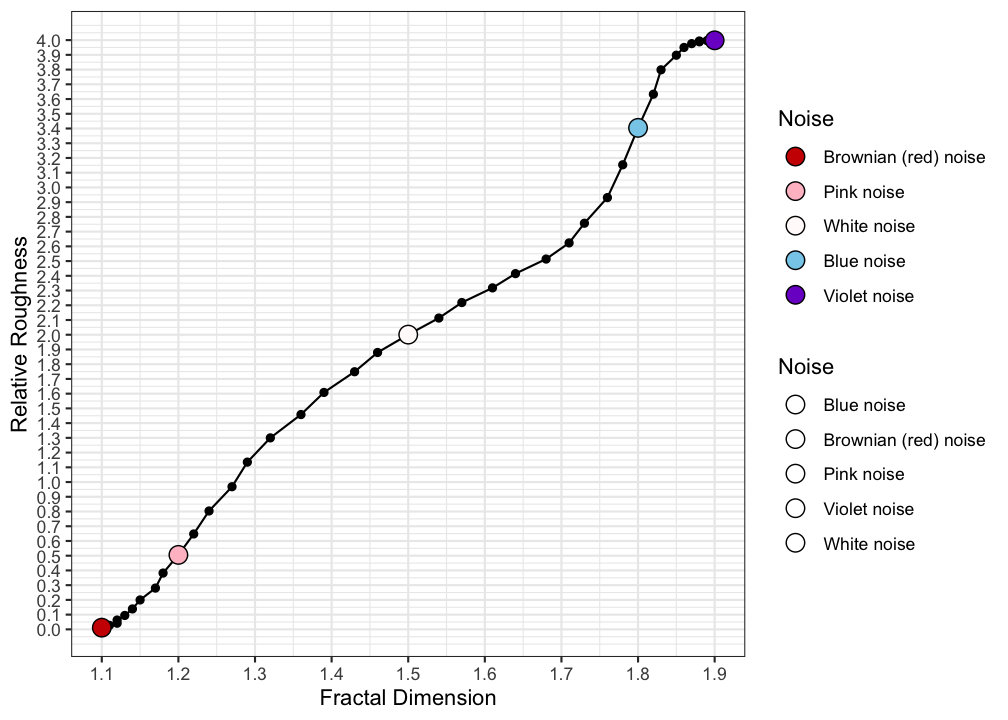
Figure 5.3: Coloured Noise versus Relative Roughness